What is correlation in the context of P&C Insurance?
What does the correlation imply?
Intuitively, we could assume correlation is a measure of how similar two Lines of Business are - this is right as far as it goes, but it may not be telling us anything useful.
Before we begin, it is essential to quantify what similarities we are referring to, pick out the important ones, and measure them correctly.
For instance, consider the total losses by calendar year for a company's Best's Schedule P lines: MM Occ and OL Occ.
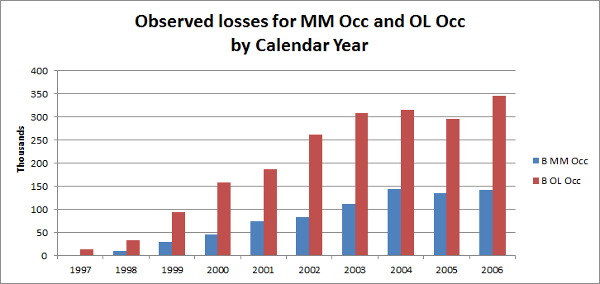
Calculating the correlation between these two series gives us a measure of 0.97.
So what?
If the two Lines of Business are modeled independently, we can obtain predictions for the losses.
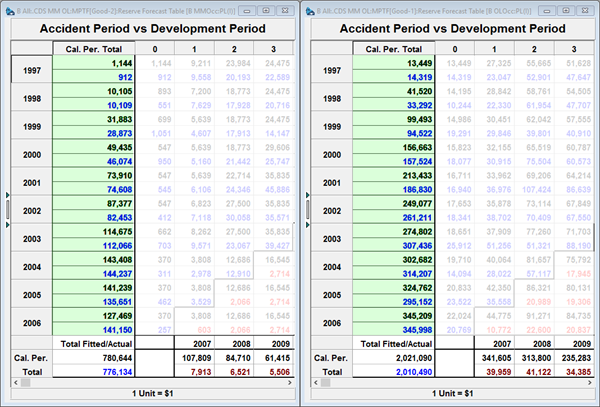
In this example, observed losses by calendar year (blue numbers) are close to what the expected mean losses (black numbers) when we have designed a model independently for both lines (calendar year totals are highlighted).
So what value does this correlation measure add that we did not know already?
Probably not much.
What if we split the annual losses for each line into two categories:
- what we already expected from our reserving model, and
- the unpredictable difference between (1) and how things actually turned out.
The correlation between the losses in category (1) are explained differently from the correlation in the differences in category (2).
The former correlation may arise from common drivers – whether internal or external – or simply as a result of unrelated trends that have similar effects (correlation is not causation after all), but any usefulness they have is negligible compared to the modeling of the data itself.
The latter correlation is more interesting as it represents the relation of the risk components and directly affects diversification credit.
Highly correlated randomness between two lines means that more risk capital is required to cover losses should they go pear-shaped.
For the sake of this example, let’s assume we separate the trends and randomness as follows:
Mean losses predicted by Probabilistic Trend Family model
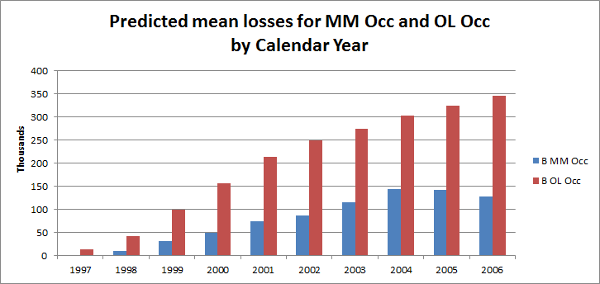
Differences between total calendar year observed losses and total calendar year predicted mean losses
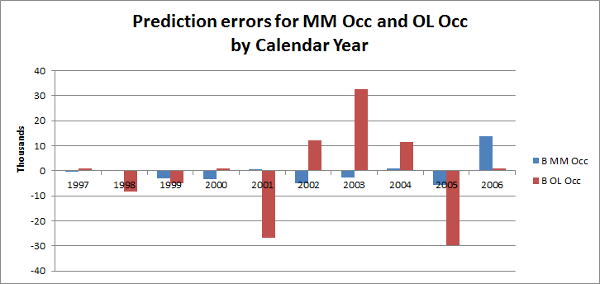
When we separate the losses into the predictable and randomness components we can see the correlation we saw in the original series is in the trends not the randomness.
This is important information.
For risk diversification purposes, by calendar year these two Lines appear hardly correlated. In terms of trends, the known component, we have incorporated all the correlation into the trend estimates and no further action needs to take place.
Correlation is always measured in the context of a base model. In the simplest case, the model is simply the mean of the data.
Note that this example is deliberately simplified to illustrate the fundamental principles we need to consider when measuring correlations. In practice, the correlations within the Multiple Probabilistic Trend Family modeling frameworks are considered at a deeper level - by cell - and therefore a more meaningful estimate of volatility measure is obtained.
Summary
In summary, we need to consider correlation in the context of what we already know about the data.
If the data can be modeled independently, as is typically the case, then correlation must be measured after the independent modeling in order to add value to the modeling process.
Certainly, one cannot mix approaches by taking a model and applying correlation directly from the data (here 0.97) as correlation measures have context.
Risk diversification is almost non-existent if the original correlation measure of 0.97 is assumed versus a post modeling correlation measure of 0.03.
