Introduction
Paraphrasing a well-known proverb: the customer complains the price is too high – unless they’ve already purchased the goods (in which case, the purchase was a steal).
In the world of risk transfer (and long-tail liability insurance and reinsurance in particular), this idea of getting the ‘lowest possible price’ does not always work in the favour of the buyer. Selecting reinsurance contracts based solely on lowest price, potentially increases the reinsurance risk – more than the difference in premiums between two potential reinsurance contracts. Premiums should be considered in the context of what a fair value is for the trading of insurance risk especially since premiums may be ceded long before the Reinsurance is called upon.
Like boasting of bargains, the concept of fair value has also been around since humans first began trading goods.
In the context of long-tail liabilities, fair value has to include a fair assessment of the mean (the expected cost) along with a risk margin (to fairly account for the additional risk where the losses exceed the mean).
With emphasis on fairness, the risk margin should also take into consideration the cases where the risk capital is not required (losses are less than the average cost).
That is, it is a probability weighted average with some loading reflecting the risk.
In addition to removing risk from the balance sheet, Reinsurance can also be used as a vehicle for managing capital efficiently. However, engaging reinsurance does not remove all risk from the balance sheet (there is the possibility that the Reinsurer defaults). If the Reinsurer is pricing fairly across all the Reinsurance agreements they issue (and not engaging in unduly risky investments) then this risk is nominal.
Naturally in life, nothing is fair, and random outcomes dictate that either the Insurer or Reinsurer feels hard done by if too much is paid (or too little).
Starting with the concept of fair value and pricing future liability streams according to their risk will result in both parties feeling good about the transaction.
An Adverse Development Cover example:
Consider a portfolio of motor vehicle insurance (CTP portfolio) with the following (simplified) structure of assets and liabilities.
The total assets the company is holding for this portfolio is 1.8B.
The total liabilities (including ALAE) are estimated as 1.25B, with risk capital of 0.25B.
The remainder, 0.3B, is shareholders equity.
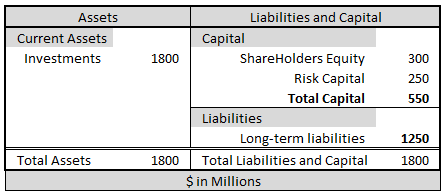
The Insurer is examining whether risk capital can be used more efficiently with the purchase of Reinsurance.
In addition, while future inflation has been steady for many years for this portfolio, the company suspects future inflation, especially medical costs, are likely to increase in the near future.
The company's objective is then to minimise risk exposure but at a fair cost (there is no advantage to the Insurer for losses to be substantially under-priced as the risk of default becomes too high).
Assume the Reinsurer identifies a PTF model, a forecast scenario, and projects a liability stream for losses and claims handling expenses (ALAE) as follows (for now the Reinsurer agrees with the Insurer's best estimate):
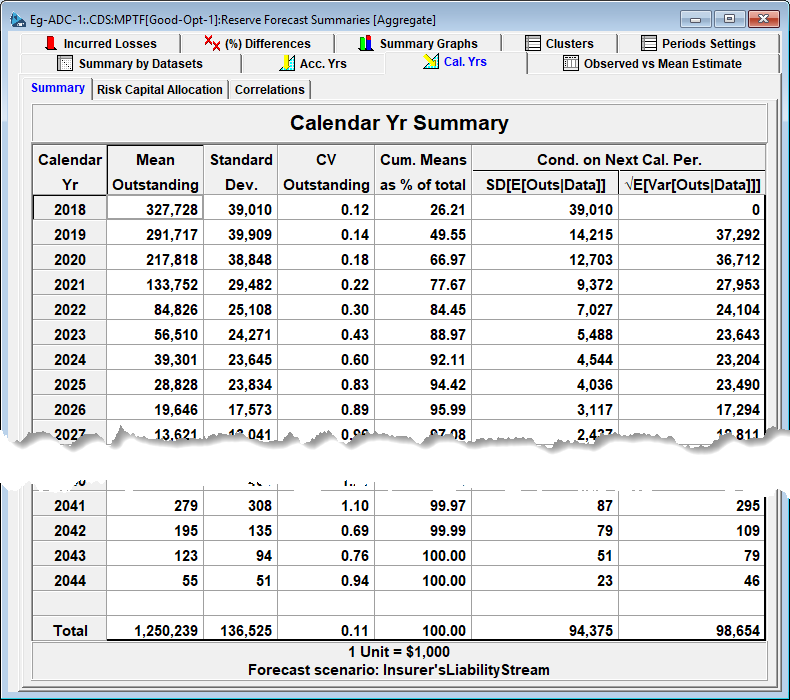
The losses are relatively volatile (for a CTP portfolio) with a total CV of 11%.
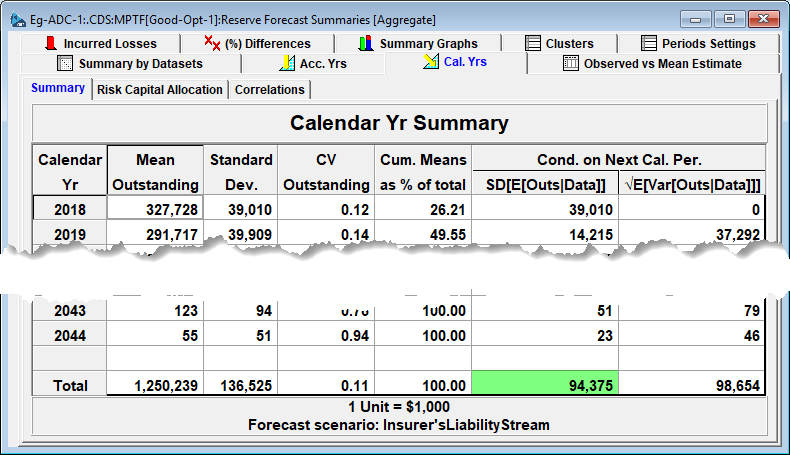
The total reserve distribution has a mean of 1.251B and a standard deviation of 0.139B. Risk capital of 250M puts the Insurer at 5% probability of loss (see below) – with an additional 100M the average loss should the risk capital be exhausted (difference between T-VaR and VaR).
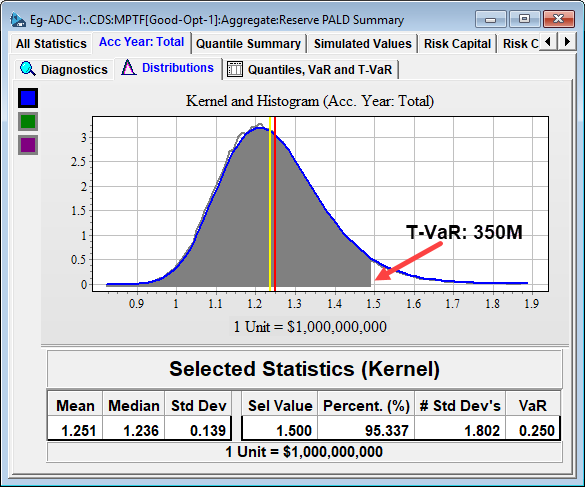
What is a fair charge for adverse development cover between 1.25B and 1.5B based on this projection of future liabilities?
Simulations are run for the correlated log-normal distributions (see PTF model) with the limits of 1.25B and 1.5B applied in the Reinsurance module.
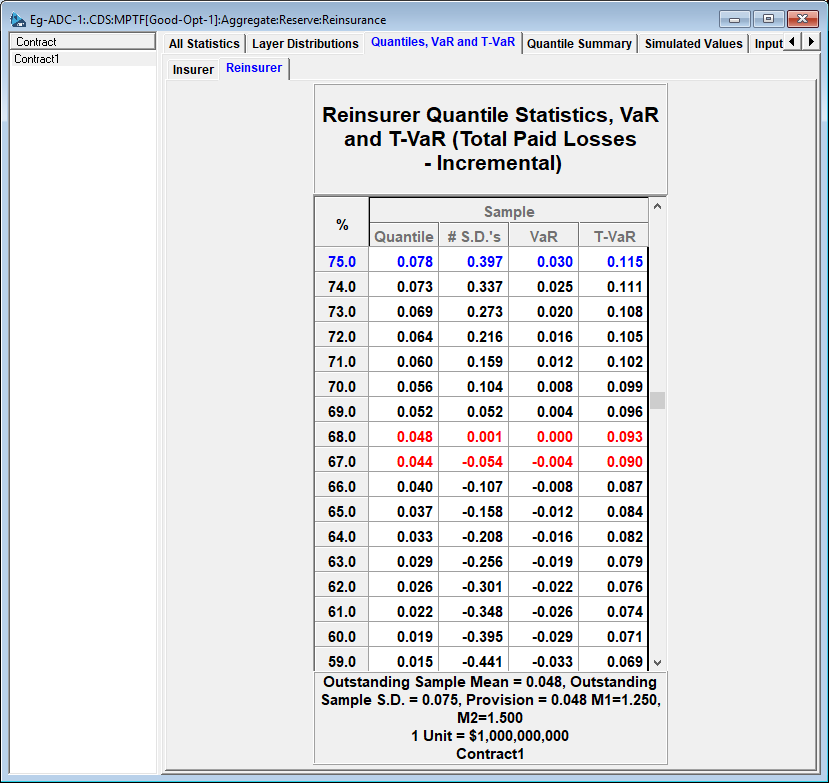
The average loss to the Reinsurer is 48M and the total average loss should the 48M be deficient (32% probability) is 93M.
A fair charge could be the weighted probabilities of:
0.68*48M + 0.32*93M.
This gives a total base premium of: 62.4M.
Allowing for administrative costs, brokerage fees, and a capital loading, the total premium for the risk capital may be assessed at 70M.
Is the risk cover worth this premium to the Insurer?
Prior to any adverse development cover, the Insurer is holding 250M to satisfy the company's level of risk appetite.
Further, the average loss to the company if the risk capital is consumed is 100M - the difference between T-VaR and VaR at the level of $1.5B$.
Let's assume the insurer wants to eliminate this risk of 100M to shareholder's equity as well.
The total risk capital the Insurer needs to hold is now 100M + RIR, where RIR is the risk of the Reinsurer becoming insolvent.
The Reinsurance module can assess the insolvency risk as well.
The probability that the Reinsurer's loss exceeds 70M is about 0.28.
The average loss to the Reinsurer should this threshold be reached is 105M.
The insolvency risk is at least 30M (0.28*105) - rounded to nearest 10M.
What is the net result?
By paying 70M in premium, the exposure to risk is dropped from 350M (risk capital plus the average loss should the risk capital be consumed) to 130M.
All (or a portion) of the difference of 50M (250 - 70 - 130) can be released into shareholder's equity.
To put this 70M premium into further context, the expected variation in mean ultimate one year from now is 94M based on the identified PTF model (conditional variation in mean ultimate highlighted below).
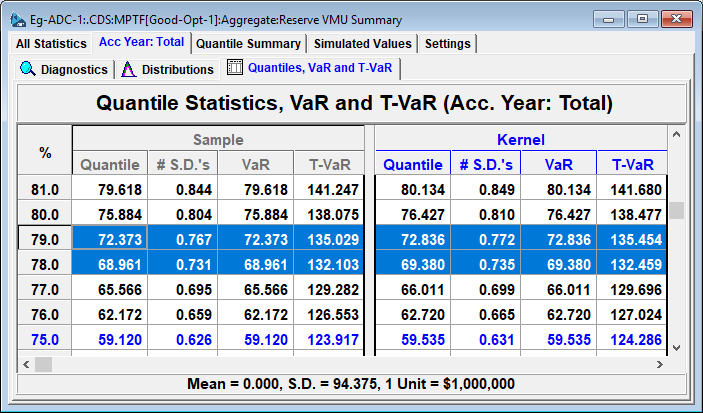
This means that, based on the Variation in Mean Ultimate simulations, there is about a 21% probability that the estimates of mean ultimate will be increased by 70M next year just based on randomness - even if the Insurer's view is correct.
By offloading the risk to the Reinsurer, the Insurer is better able to manage risk exposure and manage capital efficiently.
