Introduction
Paraphrasing a well-known proverb: the customer complains the price is too high – unless they’ve already purchased the goods (in which case, the purchase was a steal).
In the world of risk transfer (and long-tail liability insurance and reinsurance in particular), this idea of getting the ‘lowest possible price’ does not always work in the favour of the buyer. Selecting reinsurance contracts based solely on lowest price, potentially increases the reinsurance risk – more than the difference in premiums between two potential reinsurance contracts. Premiums should be considered in the context of what a fair value is for the trading of insurance risk especially since premiums may be ceded long before the Reinsurance is called upon.
Like boasting of bargains, the concept of fair value has also been around since humans first began trading goods.
In the context of long-tail liabilities, fair value has to include a fair assessment of the mean (the expected cost) along with a risk margin (to fairly account for the additional risk where the losses exceed the mean).
With emphasis on fairness, the risk margin should also take into consideration the cases where the risk capital is not required (losses are less than the average cost).
That is, it is a probability weighted average with some loading reflecting the risk.
In addition to removing risk from the balance sheet, Reinsurance can also be used as a vehicle for managing capital efficiently. However, engaging reinsurance does not remove all risk from the balance sheet (there is the possibility that the Reinsurer defaults). If the Reinsurer is pricing fairly across all the Reinsurance agreements they issue (and not engaging in unduly risky investments) then this risk is nominal.
Naturally in life, nothing is fair, and random outcomes dictate that either the Insurer or Reinsurer feels hard done by if too much is paid (or too little).
Starting with the concept of fair value and pricing future liability streams according to their risk will result in both parties feeling good about the transaction.
An Adverse Development Cover example:
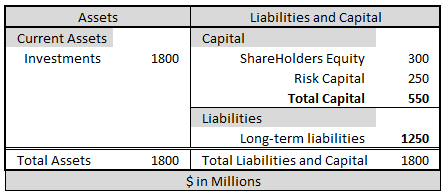
Consider a company writing six lines of business with the following (simplified) structure of assets and liabilities.
The total assets the company is holding for this portfolio is 1.8B.
The total liabilities (including ALAE) are estimated as 1.25B, with solvency risk capital of 0.25B.
Leaving shareholders' equity at 0.3B.
The Insurer is examining whether risk capital can be used more efficiently with the purchase of Reinsurance.
In addition, while future inflation has been steady for many years for this portfolio, the company suspects future social inflation, especially medical costs, are likely to increase in the near future. We will assume the reinsurer also has access to the same inflation risk profile - but with a slightly more adverse view toward the higher inflation risk.
The company's objective is then to minimise risk exposure but at a fair cost (there is no advantage to the Insurer for losses to be substantially under-priced as the risk of default becomes too high).
The Reinsurer identifies an MPTF model (based on an individual PTF model for each line and incorporating correlations between lines - as estimated from the data) and a forecast scenario which projects the following risk profile for the six lines:
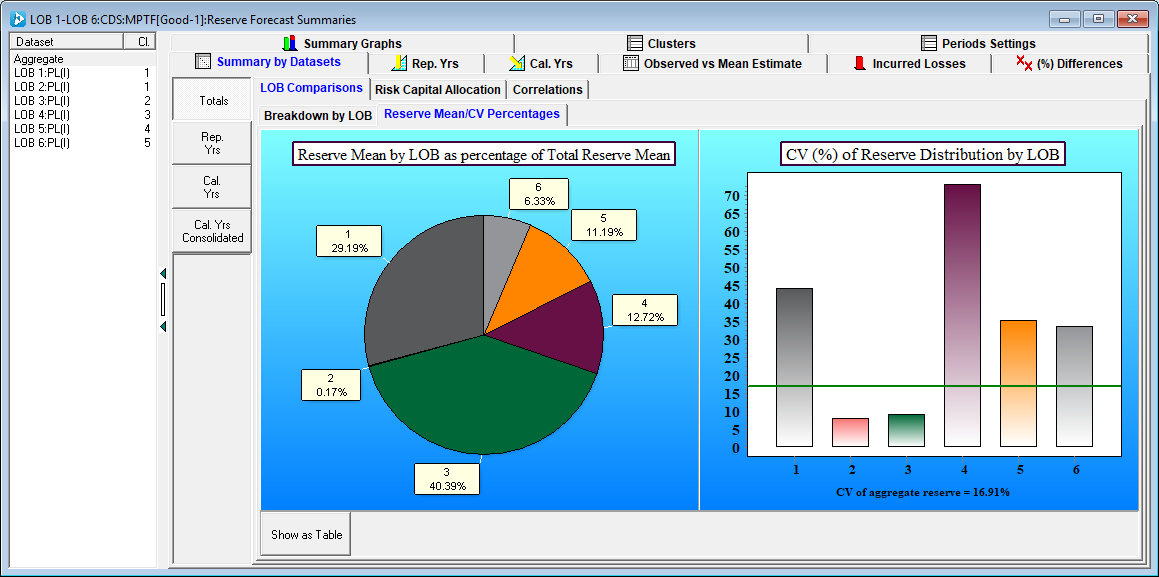
Losses are relatively volatile with a total CV of about 17%.
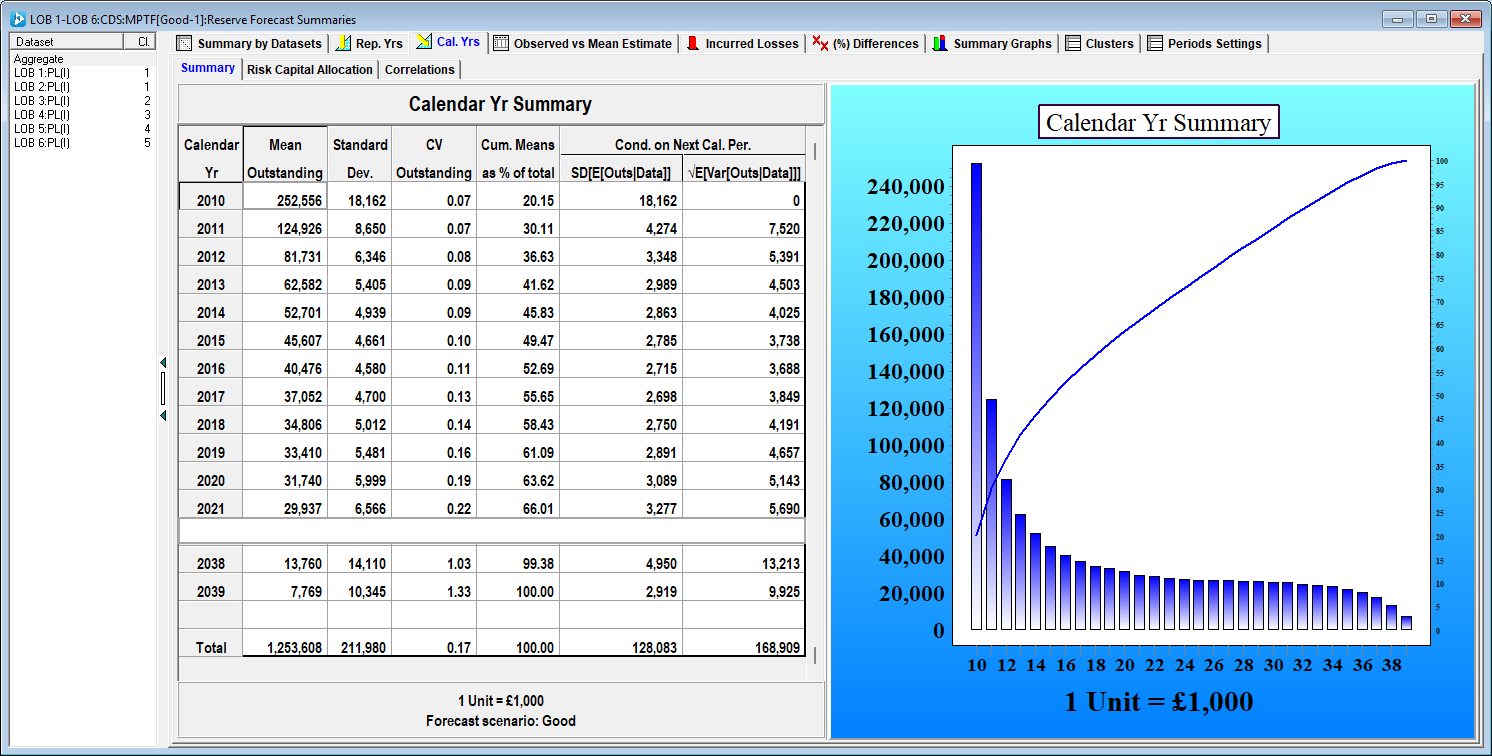
The liability stream for losses and claims handling expenses (ALAE) is projected as follows (for now the Reinsurer agrees with the Insurer's best estimate):
The Reinsurer's estimate of the total reserve distribution has a mean of 1.254B and a standard deviation of 0.212B. Risk capital of 250M puts the Insurer at 11% probability of loss (see below) – with an additional 185M the average loss should the risk capital be exhausted (difference between T-VaR and 250M).
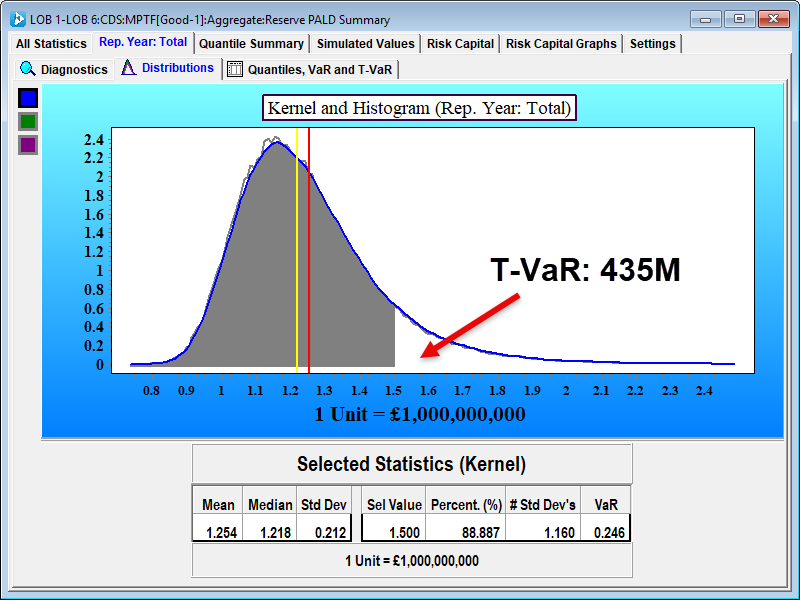
Let's assume the insurer wants to eliminate this risk of 185M to shareholders' equity as well; greatly enhancing the value of the proposition.
What is a fair charge for adverse development cover between 1.25B and 1.685B based on this projection of future liabilities?
Simulations are run for the correlated log-normal distributions (see MPTF model) with the limits of 1.25B and 1.685B applied in the Reinsurance module.
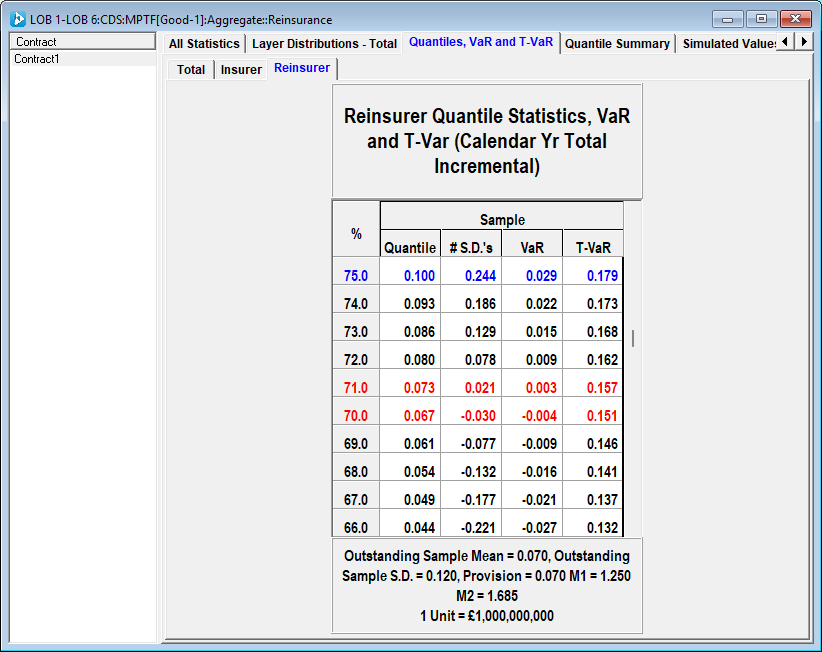
The average loss to the Reinsurer is 73M and the total average loss should the 73M be deficient (29% probability) is 157M.
A fair charge could be the weighted probabilities of:
0.71*73M + 0.29*157M.
This gives a total base premium of: 97M; ie 73M (mean) plus risk loading (24M).
Allowing for administrative costs, brokerage fees, and so forth, let's say the Reinsurer charges 105M.
Is the risk cover worth this premium to the Insurer?
Prior to any adverse development cover, the Insurer is holding 250M of shareholders' equity at risk to satisfy the company's level of risk appetite.
Further, we can calculate the average loss to the company should the 250M be consumed. It turns out this estimate is 185M meaning in the worst case scenario that the 250M is inadequate then on average an additional 185M of shareholders' equity will be needed to cover the shortfall.
Although this example is a little extreme, this is exactly why insurance companies target a solvency ratio of at least 2.
By paying the proposed premium of 105M, the risk of loss up to and including the additional 185M mentioned, is now reduced to simply the risk of the reinsurer becoming insolvent.
Obviously there are many other factors that can (and should) go into pricing including allowances for discounting, rules on commutation, than we can cover here. However, the basic principles that the price charged should reflect the actual risk transferred, protects both the cedant and the reinsurer when the prices are fair.
The next obvious question is, how much risk capital should the company continue to hold given the above risk transfer? We can consider this as being the risk capital required should the reinsurer pay out the entire premium and then fail to make good on the remaining limit. We can look at the average loss to the reinsurer should the premium be fully consumed.
Running the simulations, the probability that the Reinsurer's loss exceeds 105M is about 0.24. The average loss to the Reinsurer should this threshold be reached is 180M.
We can take the difference of 180M and 105M (namely 75M) as being the minimum risk capital that the company needs to hold should the reinsurer fail to meet its obligations.
What is the net result?
By paying 105M in premium, the shareholders exposure to risk is dropped from 435M (risk capital plus the average loss should the risk capital be consumed) to only 180M (the premium loss is guaranteed; barring arrangements for commutation etc).
The funds allocated for risk capital (250M) is reduced to 75M. The premium of 105M is paid to the reinsurer. The difference of 70M is then fully part of shareholders' equity (in the sense that the capital is less restricted for investment - rather than funds allocated in case of adverse development to the liability experience).
To put this 105M premium into further context, the expected variation in mean ultimate one year from now is 128M based on the identified MPTF model (conditional variation in mean ultimate highlighted below).
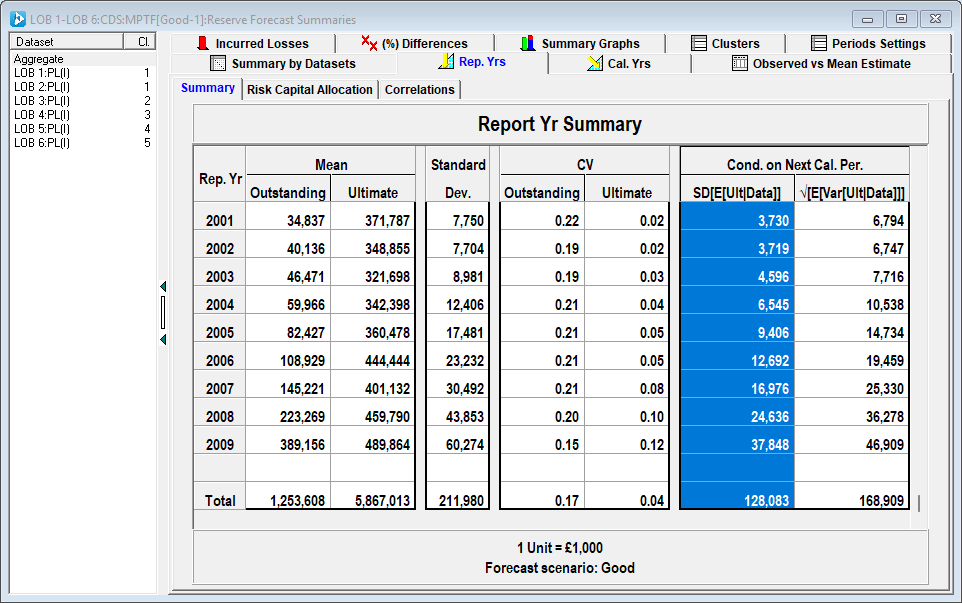
By offloading the risk to the Reinsurer, the Insurer is better able to manage risk exposure and manage capital efficiently. Risk transfer is clearly involved - the Reinsurer is 'at risk', the transfer is not just a financial instrument.
An Adverse Development Cover example: extended
A question on the above portfolio is that the adverse development cover proposed is on the aggregate of the six lines. We note that lines 2 and 3 are not very volatile. What if we only purchase reinsurance for the volatile lines?
Assuming the same risk appetite, 60M of risk capital would be required to cover the losses arising from Lines 2 and 3 by the insurer. Should that be insufficient, an additional 25M would be required (on average) to top up the risk capital for those two lines. This may be deemed an acceptable risk.
For the other four lines, which are much more volatile, let's say the company requested cover to 350M. Following the same approaches as above, we find that the reinsurer's premium is likely to be in the order of 95M. This gives an immediate indication of the risk diversification benefit as the premium is not that much lower for the four lines, versus the six lines above.
Further, it turns out when you put all the simulations through, for the same of risk capital appetite, the insurer still needs to hold 112M of risk capital (of which only 60M is actually needed for the two lines; the remainder being any excess from the reinsurance being inadequate for the four lines).
The comparable gain in capital efficiency is minimal; highlighting again the benefit of risk diversification on pricing risk transfers. Even though intuitively a company may want to hold onto less risky business when transferring risk, it can be advantageous to add those portfolios into a risk transfer to get a discount on the whole.
